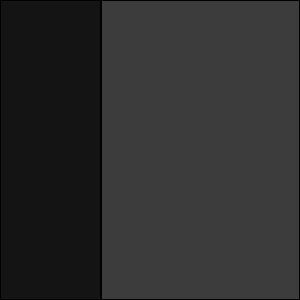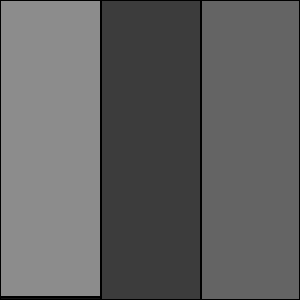Tiling and Indexes in rasdaman

When an array is inserted into rasdaman, instead of storing the whole array as it is, rasdaman first partitions it into smaller sub-arrays (tiles) and then stores them. I.e. the storage unit in rasdaman is tile, representing some part of the whole array. In order to provide quick access to the right tiles when an array is sliced/subset in a selection query, the tiles are indexed by specific index structures.

With the storage layout language extension​, rasql provides a flexible way to specify how exactly an array should be split into tiles when inserted. The storage layout language allows to pair one of several different tiling strategies with an appropriate index, in order to optimally adapt the array partitioning to the expected pattern of data access.

The rasql syntax for setting the storage layout is inherent to the insert statement:

INSERT INTO collName VALUES ...
[ TILING tilingName tilingOptions [ TILE SIZE tileSize ] ]
[ INDEX indexName ]

Tiling Schemes

No tiling

tilingName: no_tiling

As the name implies, no tiling is applied to the source array, i.e. the whole array is one tile.

Regular tiling

tilingName: regular

Regular tiling partitions the source array into a regular grid of fixed-domain tiles. This means that the array domain must be divisible by the tile domain, allowing to use a regular computed index, which is faster then indexes for non-regular tile layouts.

For example, consider inserting an array of domain [0:299,0:299] (size 300x300), and splitting into tiles of domain [0:99,0:49] (size 100x50):

insert into test
values
  marray x in [0:299,0:299] values 1c
tiling regular [0:99,0:49]
index rc_index

The resulting layout of the array as stored in the database is shown on the below image.

Aligned tiling

tilingName: aligned

Aligned tiling allows to flexibly describe the format that tiles should have. The tile configuration is expressed with a multidimensional interval of same dimensionality as the source array. Its extents along each dimension are interpreted relative to the others.

For example, if tile configuration is [ 0:29, 0:133 ], tiles will be 2-D arrays with the first dimension of size X and second dimension of size (134 / 30) * X. The specified tile size will determine the actual domain of the result tiles. E.g. below we use tile size 10000, which produces most tiles of domain [ 0:46, 0:210 ]:

insert into test
values
  marray x in [0:299,0:299] values 1c
tiling aligned [0:29,0:133]
  tile size 10000

Note that at the edge tile domain will be automatically aligned to the global array bound. No index is specified as by default the R+ tree index is used, which is perfectly suitable for this tiling scheme.

Tile configuration with non-fixed limits indicates a preference to have tiles span along some directions, e.g. the below results in tiles as large as possible along the first dimension (tile domains [ 0:299, 0:43 ]):

insert into test
values
  marray x in [0:299,0:299] values 1c
tiling aligned [0:*,0:43]
  tile size 40000

If fixed tiles are required, regular tiling can be imitated by setting tile size to match the tile configuration. For example, if the tile configuration is [ 0:29, 0:39, 0:59] and cell size is 2, then the tile size should be set to 144000. This will also result in more efficient computation of the tiling since the given tile configuration is used unchanged if 90% * tile_size < size of tile_config < tile_size (i.e., no computation is necessary). This applies equally to tile configurations with non-fixed limits.

insert into test
values
  marray x in [0:299,0:299] values 1c
tiling aligned [0:29,0:133]
  tile size 4020

The difference to regular tiling is that the tiles at the borders will be adjusted to fit in the domain in this case.

Directional tiling

tilingName: directional

With directional tiling we can model the tiling scheme according to a given direction (dimension) decomposition. Along each direction we set the preference for tile sizes along that direction, either by directly listing the limits for each tile (starting from the low, ending with the high dimension limit), or by setting a preference (with a '*') so that the tile is as large as possible in that direction.

The format of the tiling configuration for directional tiling consists of N decomposition vectors (for an N-D array): [dec1],[dec2],..,[decN]. The decX decomposition vector is a list of tile limits, e.g., 0,100,200,.. or a '*'.

The below demonstrates how to set tile limits for both directions, 0,100,299 in the first and 0,50,80,100,200,299 in the second:

insert into test
values
  marray x in [0:299,0:299] values 1c
tiling directional [0,100,299],[0,50,80,100,200,299]

This gives a preference to the second direction, i.e. tiles will be as large as possible in this direction:

insert into test
values
  marray x in [0:299,0:299] values 1c
tiling directional [0,100,299],[*]

Finally, specifying a with subtiling allows to respect the tile size and break between the given limits if the tile configuration in order to match tiles to the given tile size:

insert into test
values
  marray x in [0:299,0:299] values 1c
tiling directional [0,100,200,299],[*]
  with subtiling
  tile size 30000

Tiling areas of interest

tilingName: area of interest

This tiling scheme allows optimizing access when it is known that some areas of the array are accessed particularly often. These areas are listed as tile domains in the tile configuration, indicating the tiles that must be creating.

insert into test
values
  marray x in [0:299,0:299] values 1c
tiling area of interest [100:299,0:199],[0:49,0:49]

Without specifying a tile size, the tiles (besides those specified in the tiling configuration) will be as large as possible. Specifying a tile size will limit those other tiles, but it may also limit the tiles for the interesting areas. Several tile size limitation options allow to have a more precise control over this:

• NO_LIMIT
• REGROUP
• SUB_TILING
• REGROUP_AND_SUBTILING

Statistic tiling

tilingName: statistic

Index Types

R+ tree

indexName: rpt_index

General index structure that works with all tiling schemes.

Directory index

indexName: d_index

Directory of interval objects index like an R+ tree works with all tiling schemes.

Regular computed index

indexName: rc_index

Special index that works only with regular tiling. It should provide speed advantage over any other index, however there is a bug at the moment.